Propriétés analytiques et applications

L’étude de fonctions faisant intervenir la fonction exponentielle est essentielle, notamment lors de la modélisation de phénomènes où des grandeurs varient proportionnellement à leurs valeurs.

I. Propriétés

Pour tout réel $x$, on a $\text e^x$ > $0$.

La fonction exponentielle est strictement croissante sur ℝ.

Pour tout réel $x$, $\text e^x$ > $1$ si et seulement si $x$ > 0.

À noter

En particulier $\text e^x=1\Leftrightarrow x=0$.

Pour tout réel a et tout réel b :

$\text e^a = \text e^b$ si et seulement si $a$ = $b$

$\text e^a$ < $\text e^b$ si et seulement si $a$ < $b$

II. Tableau de variations et courbe représentative

Tableau de variation de la fonction exponentielle :

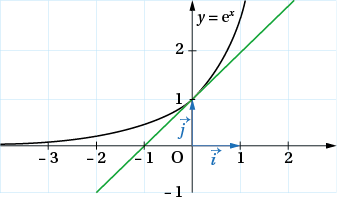
Dans le plan muni d’un repère, la courbe représentative de la fonction exponentielle admet en son point d’abscisse 0 une tangente d’équation y = x + 1.

III. Fonctions associées

À noter

Le calcul de cette dérivée fait appel à la dérivée des fonctions du type x ↦ g(ax + b)  .

Soit k un réel strictement positif.

La fonction $u\;:\; x\mapsto\text e^{kx}$ admet pour fonction dérivée $x\mapsto k\text e^{kx}$. La fonction u est strictement croissante sur ℝ.

La fonction $v\;:\; x\mapsto\text e^{-kx}$ admet pour fonction ­dérivée $x\mapsto -k\text e^{-kx}$. La fonction v est strictement ­décroissante sur ℝ.

Méthode

1)  Résoudre des équations et des inéquations

Déterminer les solutions dans R de l’équation $\text e^{2x}=\text e^x$

Déterminer les solutions dans R de l'inéquation $x\text e^x\;\gt\;x$.

Conseil

Pour résoudre ce type d’équation, on montre qu’elle est équivalente à une équation de la forme A × B = 0. De même, pour une inéquation, on montre qu’elle est équivalente à une inéquation de la forme A × B > 0.

Solution

Résolvons l'équation proposée.

$\text e^{2x}=\text e^x\Leftrightarrow \text e^{2x}-\text e^x=0$

 $\text e^{x}(\text e^x-1)=0$

$\Leftrightarrow \text e^x=0 \text{ ou } \text e^x=1$

$\Leftrightarrow x=0$.

Cette équation admet 0 pour unique solution.

Remarque : Pour tout x ∈ ℝ, \text e^x>0 donc l’équation $\text e^x=0$ n’admet pas de ­solution réelle.

Résolvons l'inéquation proposée : x\text e^x\;\gt\;x\Leftrightarrow x\text e^x-x>0~\Leftrightarrow x(\text e^x-1)>0.

On peut faire un tableau de signe ou remarquer que, pour tout x ∈ ℝ, \text e^x>1\Leftrightarrow x>0.

Les facteurs $x$ et $\text e^x-1$ sont de même signe, le produit est donc strictement positif sur ]–∞ ; 0[ ∪ ]0 ; +∞[ et nul pour x = 0. Cette inéquation admet pour solutions tous les réels non nuls.

2)  Étudier les variations d’une fonction

On considère la fonction définie sur ℝ par $f(x)=x\text e^{-x}$.

a. Déterminer la fonction dérivée de f.

b. En déduire les variations de la fonction f sur ℝ.

Conseil

Pour dériver f, on utilise la formule de la dérivée d’un produit de fonctions.

Pour les variations, on étudie le signe de f ′(x) après l’avoir factorisé.

a. Pour tout réel x, $f'(x)=1\times\text e^{-x}+x\times (-\text e^{-x})$ donc $f'(x)=(1- x)\text e^{-x}$.

b. Pour tout réel x, \text e^{-x}>0 donc f ′(x) est du signe de 1 – x. La fonction f est donc strictement croissante sur ]–∞ ; 1] et strictement décroissante sur [1 ; +∞[.

Vérifiez que vous avez bien compris les points clés des fiches 15 et 16.