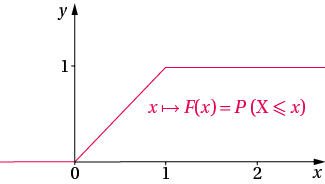Loi uniforme

Dans le cas des variables aléatoires continues, la loi uniforme prolonge la loi uniforme des variables aléatoires discrètes.

I. Densité uniforme

Définition : la densité uniforme sur l’intervalle $[a ~ ; ~ b]$ est la fonction $f$ définie sur $\mathbb{R}$ par :

$f(x)=\begin{cases} \dfrac{1}{b-a}~ \text{ si } x\in [a\;;\;b] \\ 0 \qquad \text{ si } x\notin [a\;;\;b] \end{cases}$

Justification : la fonction $f$ est visiblement positive et continue par morceaux (il y a deux points de discontinuité). De plus l’aire du domaine compris entre la courbe et l’axe des abscisses se réduit à l’aire d’un rectangle dont les dimensions sont $b-a$ et $\dfrac{1}{b-a}$ qui vaut bien $1$.

II. Loi uniforme

Définition : dire que la loi d’une variable aléatoire $X$ est la loi uniforme sur $[a ~ ; ~ b]$ signifie que la densité de $X$ est la densité uniforme. Pour tout $x \in \mathbb{R}$, sa fonction de répartition $F$ est ainsi définie

_{(N.B. : si la présente fiche est lue sous l'application, tenir le téléphone au format paysage)}

$\begin{cases} \text{si } x\le a\;,\qquad F(x)=P(X\le x)=0 \\ \text{si } x\in ]a\;;\;b[\;,~ F(x)=P(X\le x)=\dfrac{x-a}{b-a} \\ \text{si } x\ge b\;,\qquad F(x)=P(X\le x)=1 \end{cases}$

On dit souvent en abrégé que $X$ est une variable aléatoire uniforme sur $[a ~ ; ~ b]$ et on écrit : $X$$\hookrightarrow$$U([a ~ ; ~ b])$.

Espérance et variance :

$E(X) = \dfrac{a+b}{2}$ et $V(X) = \dfrac{(b-a)^2}{12}$.

Pour tous nombres $c$ et $d$ compris entre $a$ et $b$ :

$P(c \le X \le d) = \dfrac{d-c}{b-a}$.

C’est l’aire du rectangle de largeur $d-c$ et de hauteur $\dfrac{1}{b-a}$.

Méthodes

1)  Formaliser la loi uniforme sur [0 ; 1]

a. Déterminer la densité uniforme $f$ sur $[0~ ; ~ 1]$.

b. Soit $X$ une variable aléatoire uniforme sur $[0~ ; ~ 1]$. Déterminer la fonction de répartition de $X$ et la représenter graphiquement.

a. On a ici $a = 0$ et $b = 1$.

$f(x) = \begin{cases}1~\text{ si }~~x \in [0~;~1] \\ 0~\text{ si }~~x \notin [0~;~ 1]\end{cases}$

b. On trouve :

_{(N.B. : si la présente fiche est lue sous l'application, tenir le téléphone au format paysage)}

$F(x) = P(X \le x) =\begin{cases}0~~\text{si}~x\le 0 \\ x~~\text{si } x\in ]0\;;\;1[ \\ 1~\text{si}~x\ge 1 \end{cases}$

2)  Utiliser une loi uniforme

Un distributeur de boissons est électroniquement contrôlé pour verser dans le gobelet une quantité aléatoire comprise entre $190 ~ mL$ et $210 ~ mL$.

Soit $X$ la variable aléatoire égale au volume versé dans le gobelet.

1. Trouver la loi de $X$.

2. En déduire la probabilité pour que l’on ait :

a. moins de $196 ~ mL$ ; b. entre $193$ et $201 ~ mL$.

3. Quelle quantité un utilisateur obtient-il en moyenne ?

Solution

1. La quantité $X$ est un nombre pris au hasard dans l’intervalle $[190 ~ ; ~ 210]$.

Donc X suit la loi uniforme sur l’intervalle [190 ; 210].

2.

a. On cherche

$P(x \le 196) = \dfrac{196 - 190}{210 - 190} = \dfrac{6}{20} = 0,3$.

b. Cela correspond à

$P(193 \le X \le 201) =\dfrac{201 - 193}{210 - 190} = \dfrac{8}{20} = 0,4$.

3. Un utilisateur peut espérer avoir 200 mL

car $E(X) = \dfrac{190+210}{2} = 200$.