Inéquations du premier degré à une inconnue

Dans un certain nombre de problèmes numériques, comparer des grandeurs est nécessaire. Pour cela, il est souvent utile de passer par la résolution d’inéquations.

I) La leçon

1) Inégalité

$a \lt b$ signifie que $a−b$ est un nombre négatif (plus petit que 0) ou $b−a$ est un nombre positif.

$a$ et $b$ étant deux nombres réels, $a\leqslant b$ signifie que $a \lt b$ ou $a=b$.

Propriétés : quels que soit les nombres $a$, $b$, $c$, on a (ces propriétés sont également vraies pour $>$, $\leqslant$ et $\geqslant$) :

• si $a \lt b$ alors $a+c \lt b+c$;
• si $a \lt b$ et $c \gt 0$ alors $ac \lt bc$;
• si $a \lt b$ et $c \lt 0$ alors $ac \gt bc$.

Dans le cas où $c<0$, il faut inverser le sens de l’inégalité.

Si $a \gt b$, alors $a+12 \gt b+12$ ; $a−25 \gt b−25$ ; $3a>3b$ mais $−2a<−2b$.

Justification : pour prouver ces propriétés, on utilise la définition ci-dessus et les règles du signe du produit de deux nombres réels :

Exemple : Pour la première propriété : $(a+c)−(b+c)=a+c−b−c=a−b$ or $a \lt b$ donc $a−b<0$ donc $(a+c)−(b+c)<0$ donc $a+c \lt b+c$.

2) Inéquation

Une inéquation est une inégalité conditionnelle contenant une ou plusieurs inconnues représentées par des lettres. Les valeurs pour lesquelles l’inégalité est vraie sont les solutions de l’inéquation.

Résoudre une inéquation consiste à déterminer l’ensemble de ses solutions.

Les inéquations équivalentes sont des inéquations qui ont le même ensemble de solutions.

On travaille ici uniquement avec des inéquations du premier degré à une inconnue, c’est-à-dire des inéquations qui sont équivalentes à des inéquations du type : $ax \lt b$ ou $ax\leqslant b$ ou $ax \gt b$ ou $ax\geqslant b$.

Pour obtenir une inéquation équivalente à une inéquation donnée, on peut :
– règle 1 : simplifier chacun des membres, par développement ou factorisation ;
– règle 2 : ajouter ou retrancher aux deux membres une même expression littérale ;
– règle 3 : multiplier ou diviser ses deux membres par un même nombre positif ;
– règle 4 : multiplier ou diviser ses deux membres par un même nombre négatif mais en inversant le sens de l’inégalité.

Justification : ces règles découlent directement des propriétés du §1.

II) Ce qu'il faut savoir faire

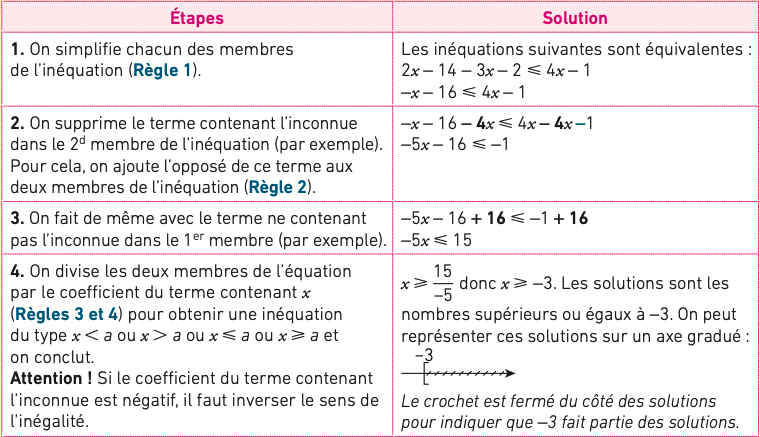
Résoudre des inéquations du premier degré à une inconnue

Exemple : résoudre l’inéquation $2(x−7)−(3x+2)\leqslant 4x−1$.

Résoudre des problèmes numériques nécessitant une mise en inéquation

Exemple : Rose et Hakim choisissent un nombre. Rose ajoute 2 au nombre choisi et multiple le résultat par 3. Hakim ajoute 5 au nombre qu’il a choisi. Rose constate qu’elle obtient un résultat plus grand que celui de Hakim. Quels nombres ont-ils pu choisir ?

III) Je m'entraine

1. Résoudre les inéquations suivantes dans IR et représenter les solutions sur un axe gradué :

a. $5−3(2x−7)>−9x−25$ ;

b. $3x− 4(2x−8) \lt x−28$ ;

c. $4x+(5−6x)\geqslant 7x+13$

2. Une salle de sport propose deux tarifs : un tarif A (abonnement annuel de 300 € et 2 € la séance) et un tarif B (abonnement annuel de 150 € et 5 € par séance).
Pour combien de séances le tarif A est-il plus avantageux que le tarif B ?