Démontrer avec le calcul littéral

Le calcul littéral permet de démontrer des propriétés sur les nombres. Pour effectuer ces démonstrations, il faut savoir démontrer que deux expressions littérales sont égales.

I) La leçon

1) Expressions littérales égales

Pour démontrer que deux expressions littérales sont égales, plusieurs propriétés existent.

2) Démontrer avec le calcul littéral

On considère le programme de calcul suivant :
Choisir un nombre - Lui ajouter 1 - Élever au carré le résultat obtenu - Retrancher au nombre obtenu le carré du nombre choisi au départ - Retrancher 1

On effectue ce programme en choisissant 5 comme nombre de départ puis 3 puis 2,5.

On obtient :

$(5+1)2−52−1=36−25−1=10$

$(3+1)2−32−1=16−9−1=6$

$(2,5+1)2−2,52−1$

$=12,25−6,25−1=5$

On constate qu’on obtient chaque fois le double du nombre choisi au départ. Ce constat (appelé conjecture) est-il vrai quel que soit le nombre choisi ? Le fait d’essayer une multitude de nombres ne permettra pas de le prouver. Il y a peut-être une exception qui invalidera la conjecture.

Une conjecture est une affirmation mathématique qui nous semble vraie mais qu’on n’a pas encore démontrée.

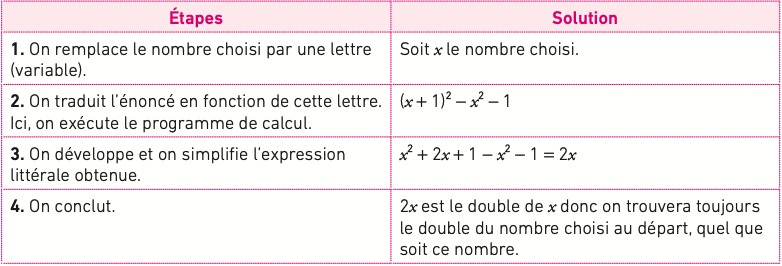
Pour prouver cette conjecture, on utilise le calcul littéral.

II) Ce qu'il faut savoir faire

Démontrer que deux expressions littérales sont égales

Exemples
a. Soit $\text{A}=(4x+2)(4x-2)$ et $\text{B}=(5x-2)(2x+3)-(11-6x)\times{x+2}$. Démontrer que A = B.

b. Soit $\text{C}=56x^2-40x-12$ et $\text{D}=(7x-7)(8x+2)+2(x+1)$. Démontrer que C = D.

Remarque : dans certains cas, on peut aussi démontrer que la différence entre les deux expressions est égale à 0.

Démontrer une conjecture portant sur les nombres § 1

III) Je m'entraine

1. a. Soit $\text{A}=(12x+4)(2x-3)$ et $\text{B}=(4x-6)(6x+2)$. Démontrer que A = B.
b. Soit $\text{C}=-24-3(2x-7)-(4x+1)(x-3)$ et $\text{D}=(3x-2)^2-(13x^2+4-17x)$. Démontrer que C = D.

2. Voici un programme de calcul : choisir un nombre, lui ajouter 3, retrancher 3 au nombre choisi au départ. Multiplier les deux résultats obtenus et ajouter 9 au produit obtenu. Appliquer ce programme avec les nombres 2 ; −1 et 7. Quelle conjecture peut-on faire ? La démontrer.

3. Tracer un segment [AB] tel que AB = 7 cm. Placer un point M sur [AB]. Tracer un triangle équilatéral ACM et un triangle équilatéral MDB. Démontrer que, quelle que soit la position du point M, la somme des périmètres des triangles ACM et MDB est égale à 21 cm.