Volume et contenance

Les concepts de volume et de contenance permettent de caractériser l’espace occupé par des objets en trois dimensions.

I) La leçon

1) Mesure du volume ou de la contenance d’un solide

Le volume d’un solide caractérise l’espace qu’il occupe. Lorsque ce volume correspond à la quantité de liquide, d’air... que le solide peut contenir, on utilise parfois le terme de contenance.

Une unité de volume étant choisie, la mesure du volume d’un solide est le nombre d’unités nécessaires pour le remplir entièrement.

Conséquence : la mesure est un nombre réel qui dépend du choix de l’unité de mesure.

Exemple : En cm3, la mesure du volume de ce cube est 27 (il faut 27 cubes d’arête 1 cm pour le remplir). En mm³, la mesure de son volume est 27 000 (il faut 27 000 cubes d’arête 1 mm pour le remplir).

On dit aussi que le volume de ce cube est égal à 27 cm³ ou à 27 000 mm³. En effet, un cube de 1 cm d’arête contient 1 000 cubes de 1 mm d’arête.

On a donc l’égalité 27 cm³ = 27 000 mm³.

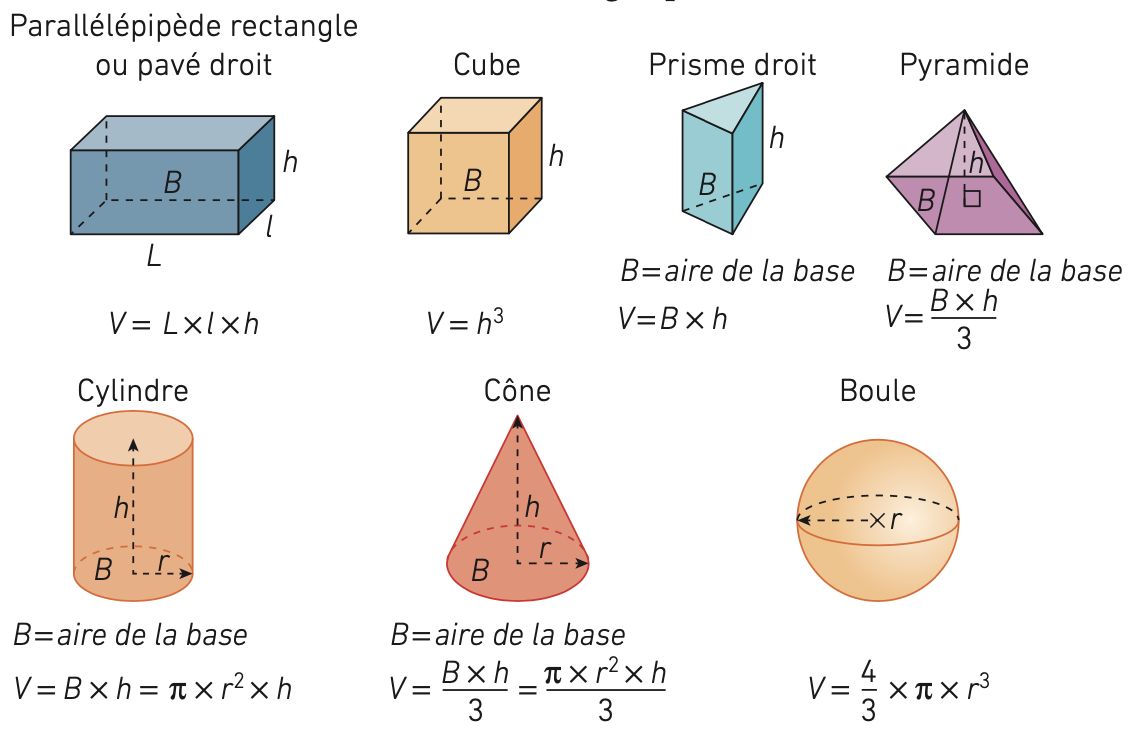
2) Volume de solides usuels

Dans la suite, le volume du solide est désigné par $V$.

3) Unités de volume et de contenance

Les unités de volume et de contenance sont définies par le Système international d’unités (SI). L’unité principale est le mètre-cube (m³) égal au volume d’un cube de 1 m de côté. Les différentes unités sont liées entre elles par des relations liées au système décimal.

Les contenances sont souvent exprimées dans un système dont l’unité est le litre (L).

Les deux systèmes d’unité sont liés par l’égalité 1 L = 1 dm³.

Ces deux systèmes sont présentés dans le tableau suivant qui peut être utilisé pour effectuer des conversions d’unités (avec les abréviations usuelles).

Certaines unités sont peu utilisées (km³, hm³, par exemple).

• Dans le premier système (en m³), une unité située à gauche d’une autre unité dans le tableau vaut 1 000 fois cette unité.

1 m³ = 1 000 dm³= 1 000 000 cm³ = 1 000 000 000 mm³

• Dans le second système (en L), une unité située à gauche d’une autre unité dans le tableau vaut 10 fois cette unité (comme pour les longueurs).

1 hL = 10 daL= 100 L = 1 000 dL = ...

II) Ce qu'il faut savoir faire

Calculer le volume de solides usuels ou de solides décomposables en solides usuels

On utilise les formules connues pour les solides usuels et des méthodes identiques à celles décrites pour les aires pour les autres solides.

Calculer une longueur ou une aire dans un solide élémentaire connaissant son volume

On utilise également les formules connues.

Effectuer des conversions d’unités (dans les deux systèmes, fondés sur le m³ et les L)

On utilise les mêmes méthodes que pour les conversions d’unités d’aire.

III) Je m'entraine

1. a. Exprimer le volume V de ce solide en fonction de $h$.

b. V = 314 cm³. Quelle est la hauteur $h$ du cône ?

2. Effectuer les conversions suivantes :

a. 4,65 m³ = ... cm³ ;

b. 1 275 mm³ = ... dm³ ;

c. 480 cm³ = ... L ;

d. 0,000045 m³ = .... cL ;

e. 300 560 L = .... m³ ;

f. 437 mL = .... cm³.