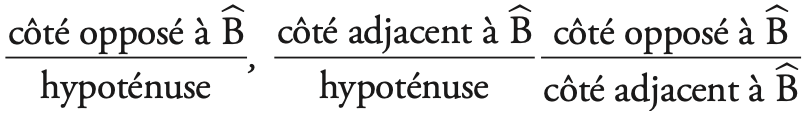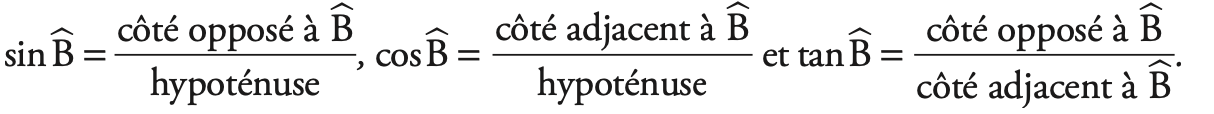Les relations trigonométriques dans un triangle rectangle relient la mesure des angles aigus d’un triangle rectangle avec les longueurs des côtés de ce triangle. Elles permettent de calculer des longueurs de segments et des mesures d’angles.
I) La leçon
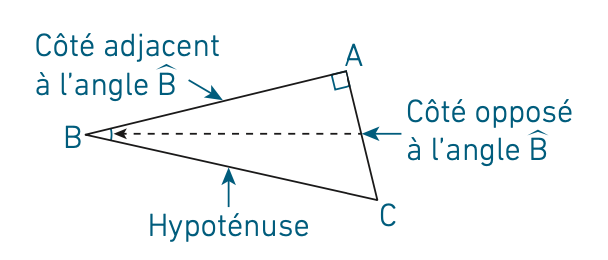
1) Vocabulaire
2) Propriété – Définition
Dans un triangle rectangle où est un angle aigu du triangle, les rapports :
ne dépendent que de la mesure de l'angle .
Cela permet de définir le sinus de l’angle (noté sin ), le cosinus de l’angle (noté cos ) et la tangente de l’angle (noté tan ).
En écrivant « côté opposé à sur hypoténuse », on fait un abus de langage : on devrait écrire « longueur du côté opposé à B » et « longueur de l’hypoténuse ».
tan(B) = sin (B) / cos (B)
Comme l’hypoténuse d’un triangle rectangle est le plus grand côté, le sinus et le cosinus d’un angle aigu d’un triangle rectangle sont compris entre 0 et 1.
Avec une calculatrice, le sinus, le cosinus et la tangente d’un angle de mesure donnée se déterminent en utilisant les touches sin, cos et tan.
Les relations trigonométriques dans un triangle rectangle permettent de calculer la longueur d’un côté d’un triangle rectangle.
Condition d’utilisation : connaitre un angle (autre que l’angle droit) d’un triangle rectangle et la longueur d’un autre côté de ce triangle.
II) Ce qu'il faut savoir faire
Calculer une longueur d’un côté d’un triangle rectangle en utilisant les relations trigonométriques dans le triangle rectangle
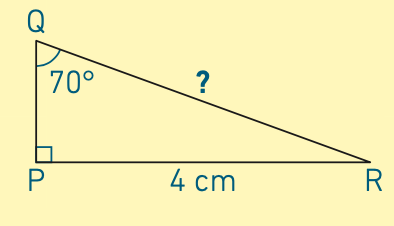
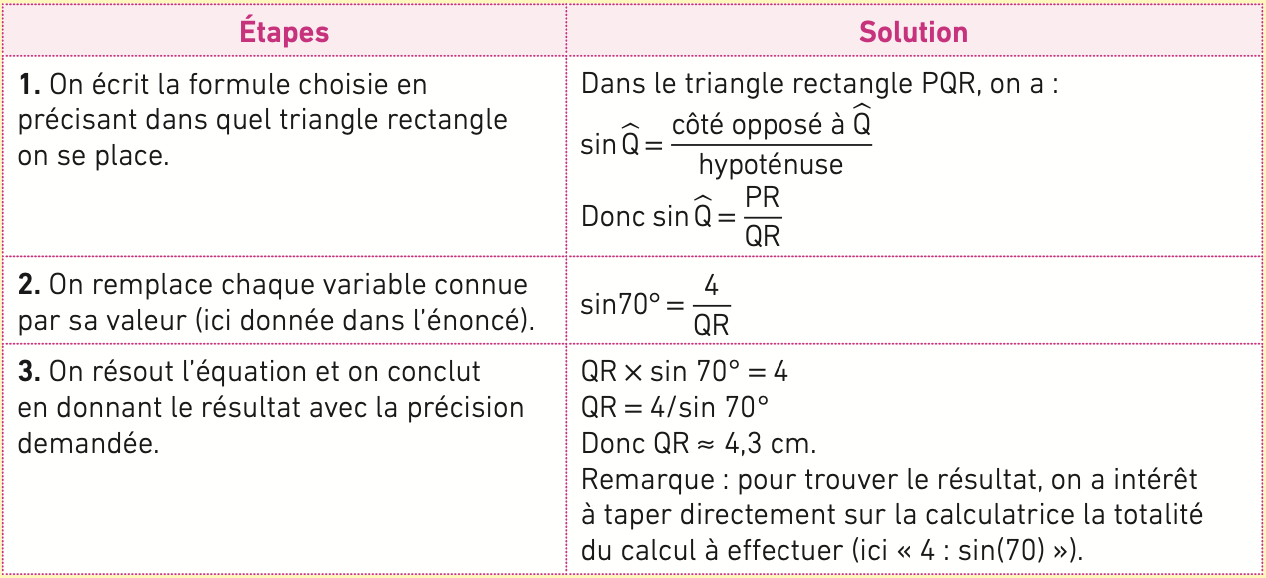
Exemple : en utilisant les informations portées sur le dessin ci-dessous, calculer une valeur approchée de QR à 0,1 cm près.
Travail préalable : on s’assure qu’on a les conditions des relations trigonométriques dans le triangle rectangle.
C’est le cas ici :
– on dispose d’un triangle rectangle dont on cherche la longueur d’un côté ;
– on connait la longueur d’un autre côté du triangle (QR) et la mesure d’un angle ().
On choisit la formule trigonométrique à utiliser : c’est le lien entre l’angle connu, le côté dont on cherche la longueur et le côté dont on connait la longueur qui permet de faire ce choix. Ici, on cherche la longueur de l’hypoténuse et on connait la longueur du côté opposé (PR) à l’angle connu (). Il faut donc utiliser le sinus de l’angle connu.
Une fois le résultat trouvé, on peut, dans certains cas, s’assurer qu’il est plausible en vérifiant que la longueur de l’hypoténuse est plus grande que la longueur des autres côtés connus. C’est le cas ici : 4,3 > 4.
III) Je m'entraine
Quand c’est possible, calculer un arrondi à 0,1 unité de longueur près de ED. (Les mesures sont exprimées dans la même unité.)