Démontrer que deux triangles sont égaux (superposables) permet de prouver que des longueurs de segments sont égales ou que des angles sont égaux.
I) La leçon
1) Définition
Deux triangles sont égaux s’ils sont superposables, c’est-à-dire si l’un des triangles est image de l’autre par une isométrie.
On parle aussi de triangles isométriques.
2) Propriétés
Trois propriétés permettent de caractériser des triangles égaux (elles sont appelées « cas d’égalité des triangles »).
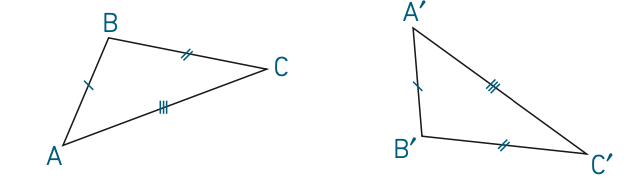
Cas d’égalité 1 : deux triangles sont égaux si et seulement si les longueurs des trois côtés d’un triangle sont respectivement égales aux longueurs des trois côtés de l’autre triangle.
Exemple : Les triangles ABC et A′B′C′ ci-dessous sont égaux.
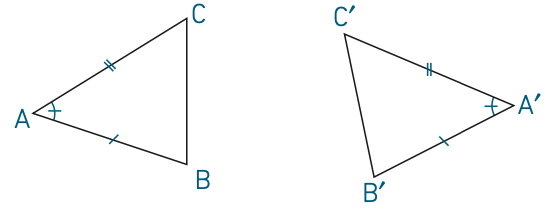
Cas d’égalité 2 : deux triangles sont égaux si et seulement si un angle d’un triangle est égal à un angle d’un autre triangle et si les longueurs des côtés formant ces angles sont respectivement égales.
Exemple : Les triangles ABC et A′B′C′ ci-dessous sont égaux.
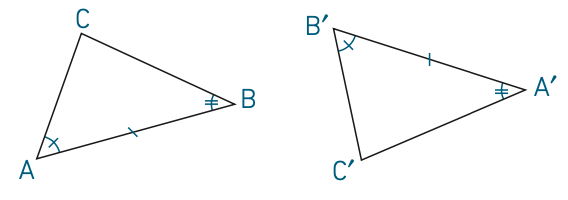
Cas d’égalité 3 : deux triangles sont égaux si et seulement si deux angles d’un des triangles sont respectivement égaux à deux angles de l’autre et les longueurs des côtés communs à ces deux angles sont égales.
Exemple : Les triangles ABC et A′B′C′ ci-dessous sont égaux.
Ces cas d’égalité des triangles permettent de démontrer que des longueurs de côtés de triangles sont égales. Cela suppose de savoir démontrer que deux triangles sont égaux.
II) Ce qu'il faut savoir faire
Démontrer que deux segments sont de même longueur en utilisant les propriétés des triangles égaux
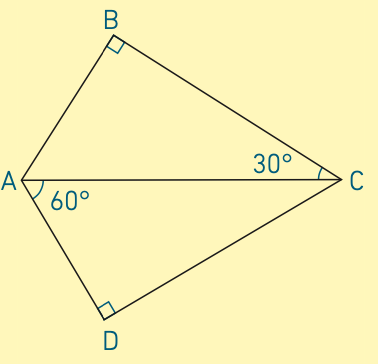
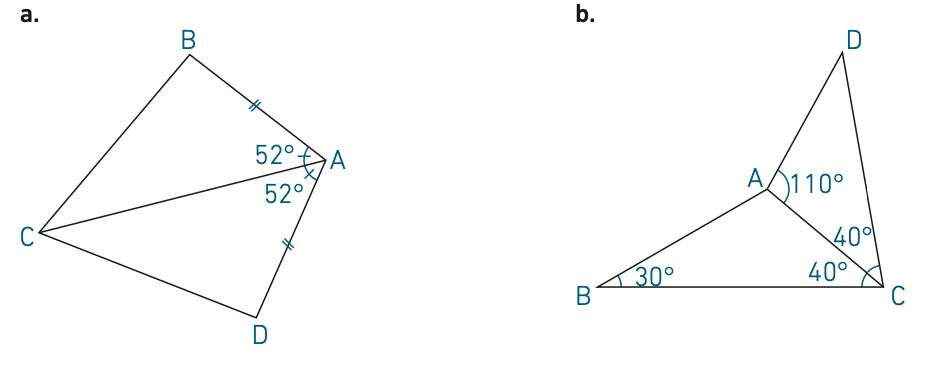
Exemple : en utilisant les informations portées sur le dessin ci-dessous, démontrer que AB = AD.
III) Je m'entraine
En utilisant les informations portées sur chacun de ces dessins, démontrer que BC = DC.