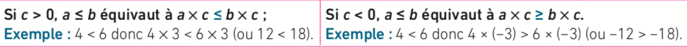Nombres réels : comparaison et calcul

La maitrise du calcul algébrique suppose une bonne connaissance des propriétés relatives à la comparaison et au calcul sur les nombres réels. Elles sont rappelées dans cette fiche.

I) Leçon

1) Opposé et inverse d’un nombre réel

$a$ est un nombre réel. L’opposé de $a$ est le nombre qui ajouté à $a$ donne 0 comme résultat. $−a$ est donc l’opposé de $a$.

Exemple : $−2,7$ est l’opposé de $2,7$ et $2,7$ est l’opposé de $−2,7$.

Attention :
$−a$ ne désigne pas forcément un nombre négatif. Si $a = −2,7$, alors $−a = −(−2,7) = 2,7$ (qui estun nombre positif). D’une façon générale, si a > 0 alors −a < 0 et si a < 0, alors −a > 0.

$a$ est un nombre réel non nul. L’inverse de $a$ est le nombre qui multiplié par $a$ donne $1$ comme résultat. $\frac{1}{a}$ est donc l’inverse de $a$.

Exemple : $\frac{1}{3}$ est l’inverse de $3$ et $3$ est l’inverse de $\frac{1}{3}$. Cela correspond aussi au fait que $\frac{1}{\frac{1}{3}} = 3$.

2) Distance d'un nombre à $0$

Soit $a$ un nombre réel :

• si $a \geq 0$, la distance de $a$ à $0$ est égale à $a$ ;
• si a < 0, la distance de $a$ à $0$ est égale à $−a$.

La distance de $3$ à $0$ et de $−3$ à $0$ est égale à $3$.

3) Addition et multiplication

A) Somme de deux nombres réels $a$ et $b$

Si $a$ et $b$ sont de même signe, leur somme a le même signe et sa distance à $0$ est la somme de leurs distances à $0$.

Exemple : $(−5) + (−3) = (−8)$ ; on écrit aussi $−5 + (−3) = −8$ ou $−5 − 3 = −8$.

Si $a$ et $b$ sont de signes contraires, leur somme a le même signe que celui qui a la plus grande distance à $0$ et sa distance à $0$ est la différence de leurs distances à $0$.

Exemple : $(−5) + (3) = (−2)$ ; on écrit aussi $(−5) + 3 = −2$ ou $−5 + 3 = −2$.

B) Produit de deux nombres réels $a$ et $b$

Si $a$ et $b$ sont de même signe, leur produit est positif et sa distance à $0$ est le produit de leurs distances à $0$.

Exemple : $(−5) \times (−3) = (+15)$ ; on écrit aussi $(−5) \times (−3) = 15$.

Si $a$ et $b$ sont de signes contraires, leur produit est négatif et sa distance à $0$ est le produit de leurs distances à $0$.

Exemple : $(−5) \times (+3) = (−15)$ ; on écrit aussi $(−5) \times 3 = −15$ ou $−5 \times 3 = −15$.

Dans l’ensemble des nombres réels :
- soustraire $b$ de $a$ revient à ajouter l’opposé de $b$ à $a$ : $a − b = a + (−b)$ ;
- diviser $a$ par $b$ (avec b ≠ 0) revient à multiplier $a$ par l’inverse de $b$ : $a : b = a \times \frac{1}{b} = \frac{a}{b}$.

C) Propriétés de l’addition et de la multiplication

Dans la suite, $a$, $b$ et $c$ sont des nombres réels.

L’addition et la multiplication sont :

• commutatives : $a + b = b + a$ et $a \times b = b \times a$ ;
• associatives : $a + (b + c) = (a+b) + c = a + b + c$ et $a \times(b \times c) = (a \times b) \times c = a \times b \times c$ ;
• munies d’un élément neutre ($0$ pour l’addition, $1$ pour la multiplication) : $a + 0 = 0 + a = a$ ; $a \times1 = 1 \times a = a$.

De plus, la multiplication est :

• munie d’un élément absorbant : $(0) : a \times 0 = 0 \times a = 0$ ;
• distributive sur l’addition : $a \times (b + c) = (a \times b) + (a \times c)$.

4) Ordre et addition

$a$, $b$, $c$ et $d$ sont des nombres réels :

5) Ordre et multiplication

$a$, $b$ et $c$ sont des nombres réels :

L’ordre est inversé lorsqu’on multiplie par un nombre négatif.

Cas particulier : $a$ et $b$ sont des nombres réels : si $a \leq b$, alors $−a \geq −b$ (on multiplie chaque nombre par $−1$).

Exemple : 3 < 7 et −3 > −7

Le passage aux opposés s’accompagne d’un changement de sens de l’inégalité.

II) Ce qu'il faut savoir faire

➢ Utiliser les propriétés relatives aux opérations et à l’ordre sur les nombres réels pour faire des raisonnements ou traiter des calculs

III) Je m'entraîne

1. Quels sont les inverses et les opposés de $7$ ; $-7$ ; $\frac{1}{7}$ ; $-\frac{3}{4}$ ; $\pi$.

2. Calculer : a. $5 + (−7)$ ; b. $(−5) − (−7)$ ; c. $\pi - \left (-\frac{\pi}{4} \right ) - \frac{\pi}{2}$

3. Calculer : a. $5 \times (−7)$ ; b. $(−5) \times (−7)$ ; c. $\pi : \left (-\frac{\pi}{4} \right )$

4. On sait que a > b. Compléter : a. $−a\ldots−b$ ; b. $a + 5 \ldots b + 5$ ; c. $a − 5 \ldots b − 5$ ; d. $(−3) \times a \ldots (−3) \times b$ ; e. $- \frac{a}{5} \ldots - \frac{b}{5}$