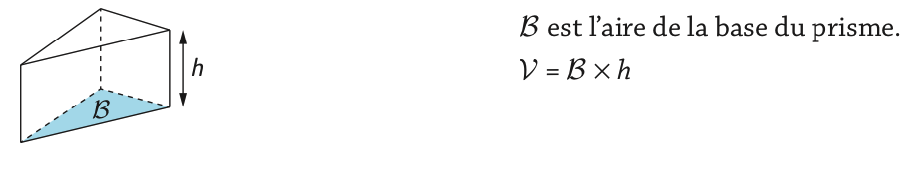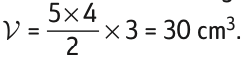Le volume des solides usuels se calcule à l’aide de formules qu’il est conseillé de mémoriser.

1 - Apprendre le cours

On désigne par V le volume d’un solide dans les formules du cours.

A - Cube

a84cd7bd-eaf5-499a-b786-8a433e0c3f54

Exemple
Le volume d’un cube dont l’arête mesure 1,5 cm est : V = 1,5³ = 3,375 cm³.

B - Parallélépipède rectangle (ou pavé droit)

7c8d6b83-e38c-48e4-ac6e-07f3f80784a0

Exemple
Le volume d’un parallélépipède rectangle dont les dimensions sont 5 cm, 4 cm et 3 cm est : V = 5 × 4 × 3 = 60 cm³.

C - Prisme droit

a764b78d-0acf-42e2-944e-1c39299c01b4

Exemple

Le volume d’un prisme droit de hauteur 3 cm et dont la base est un triangle rectangle de côtés 5 cm et 4 cm (côtés de l’angle droit) est :

1525107a-7169-4883-828f-e4e0d0c23d20

D - Pyramide

4dd27e76-8761-48e2-b668-c374ecec38ec

Exemple
Le volume d’une pyramide dont la base est un carré de côté 7 m et de hauteur 9 m est : V = (1/3) x 7² x 9 = 147 m³

E - Cylindre de révolution

c27f47b4-d020-461c-a818-7268b0d6d461

Exemple
Le volume d’un cylindre de rayon 5 cm et de hauteur 2 cm est : V = π × 52 × 2 ≈ 157 cm3 (valeur arrondie à l’unité).

F - Cône de révolution

eec31d0e-6e2a-4ab1-91c3-04bb4a893b05

Exemple

Le volume d’un cône de révolution dont le rayon de la base mesure 14 mm et la hauteur 6 mm est : V = (1/3) × π × 14² × 6 ≈ 1 232 mm³ .

G - Boule

fe22ed46-8754-438f-830d-54e2ee8a851d

Exemple
Le volume d’une boule de rayon 1,2 cm est : V = (4/3) × π × 1,2³ ≈ 7,2 cm³ .

H - Masse volumique

La masse volumique d’un corps est la masse par unité de volume de ce corps.
La masse volumique s’exprime en général en g/cm³ ou en kg/dm³.

Exemple
La masse volumique du cuivre est de 8,9 kg/dm³. Cela signifie que 1 dm³ de cuivre a une masse de 8,9 kg.

Méthode : comment calculer le volume d'un objet composé de plusieurs solides ?

Énoncé :

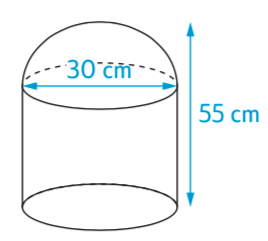
6aeaf4f5-3f83-4d31-a117-260ef066ca74

Une entreprise doit construire des plots en béton à installer au bord des trottoirs. Ces plots sont formés d’un cylindre de révolution surmonté d’une demi- boule de même diamètre. Le diamètre du cylindre est 30 cm. La hauteur totale du plot est 55 cm. Calculer, en cm3, le volume de béton nécessaire à la construction de ce plot. Arrondir à l’unité.

Réponse :

Calculez le volume de chacun des solides qui compose l’objet, puis faites leur somme.

On calcule le rayon du cylindre et de la demi-boule : rayon = 30 ÷ 2 = 15 cm.
On calcule la hauteur du cylindre : hauteur = 55 − 15 = 40 cm.
On calcule le volume V₁ du cylindre : V₁ = π × 15² × 40 ≈ 28 274,3 cm³.
On calcule le volume V₂ de la demi-boule : V₂ = (1/2) x (4/3) × π × 153 ≈ 7 068,6 cm³.
On calcule le volume du plot : V = V₁ + V₂ = 28 274,3 + 7 068,6 = 35 342,9 cm³.

2 - Appliquer le cours

EXERCICES

1. a. Calculer, en litres, le volume d’un cube d’arête 16 cm.

b. Calculer, en cm3, le volume d’un parallélépipède rectangle dont les dimensions sont 7 cm, 2,5 cm et 3,1 cm.

c. Une pile est un cylindre de 10 mm de diamètre et de 4 cm de hauteur. Calculer, en cm³, le volume de la pile.

d. Calculer, en m3, le volume d’un prisme droit de hauteur 3 m et dont la base est un triangle rectangle dont les côtés de l’angle droit mesurent 2 m et 0,5 m.

e. Calculer le volume d’un cône de rayon 6 dm et de hauteur 10 dm. Arrondir au dm3.

2. Une boîte alimentaire a la forme d’un parallélépipède rectangle. Sa base est un carré de côté 7 cm et sa hauteur mesure 21 cm. La boîte est remplie de soupe aux deux tiers de sa hauteur. Calculer le volume de soupe contenu dans la boîte.

3. Parmi les solides suivants, quel est celui qui a le plus grand volume ?
- A un parallélépipède rectangle de dimensions 6 cm, 4 cm, 2 cm ;
– B un cube d’arête 3 cm ;
– C un cylindre de rayon 3 cm et de hauteur 2 cm.

4. La balise ci-dessous est formée d’une demi-boule surmontée d’un cône de révolution de sommet A. Le segment [BC] est un diamètre de la base du cône et le point O est le centre de cette base. On donne AO = BC = 6 dm. Calculer le volume de la balise. Arrondir à 0,1 dm³.

6c84f1e8-5281-4dce-b7a2-79799908adf6

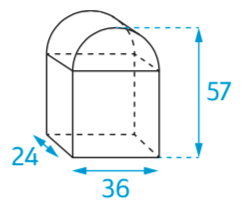
5. Voici le schéma d’une borne kilométrique au bord d’une route. La face avant est un rectangle surmonté d’un demi-disque.

1e9ba127-916e-4e72-bed0-6b2673a8db08

La borne mesure 57 cm de hauteur totale, 36 cm de largeur et 24 cm de profondeur. Quel est le volume de la borne, en dm³ ? Arrondir à l’unité.

6. Calculer la masse d’un cube d’argent d’arête 2 cm (masse volumique de l’argent : 10,5 g/cm³).

7. Une péniche a un chargement de sable en forme de parallélépipède rectangle d’une longueur de 30 m, d’une largeur de 5,2 m et d’une hauteur de 0,9 m. Sachant que la masse volumique du sable est 1,8 t/m³, quelle est la masse de sable exprimée en quintaux ?

CORRIGÉ

1. a. Volume du cube : 163 = 4 096 cm³.

b. Volume du parallélépipède rectangle : 7 × 2,5 × 3,1 = 54,25 cm³.

c. Rayon de la pile : 10 ÷ 2 = 5 mm = 0,5 cm.
Volume de la pile : π × 0,52 × 4 ≈ 3,14 cm³.

d. Aire de la base du prisme : (2 x 0,5) / 2 = 0,5 m².
Volume du prisme : 0,5 × 3 = 1,5 m³.

e. Volume du cône : (1/3)× π × 62 × 10 ≈ 377 dm³.

2. Hauteur de soupe : 21 × (2/3) = 14 cm

Volume de soupe : 7² × 14 = 686 cm³.

3. Volume du parallélépipède rectangle : 6 × 4 × 2 = 48 cm³. Volume du cube : 33 = 27 cm³.
Volume du cylindre : π × 32 × 2 ≈ 57 cm³.
C’est le cylindre qui a le plus grand volume.

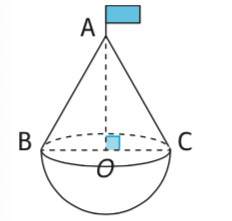
4. Volume du cône : 31 × π × 3² × 6 = 18π dm³.

Volume de la demi-boule : (1/2) x (4/3) × π × 3³= 18π dm³.

Volume de la balise : 18π + 18π = 36π dm³ ≈ 113,1 dm³.

5. Hauteur du parallélépipède rectangle : 57 − 18 = 39 cm.

Volume du parallélépipède rectangle : 36 × 24 × 39 = 33 696 cm3 = 33,696 dm³. Volume du demi-cylindre : (π × 18² × 24) ÷ 2 ≈ 12 215 cm³, soit 12,215 dm³. Volume de la borne : 33,696 + 12,215 = 45,911 dm³, donc 46 dm³ en arrondissant au dm³.

6. Volume du cube : 2³ = 8 cm³. Masse du cube : 10,5 × 8 = 84 g.

7. Volume du sable : 30 × 5,2 × 0,9 = 140,4 m³.
Masse du sable : 1,8 × 140,4 = 252,72 tonnes = 2 527,2 quintaux.

Les volumes et la masse volumique - Concours adjoint administratif Etat