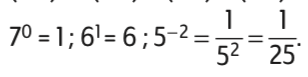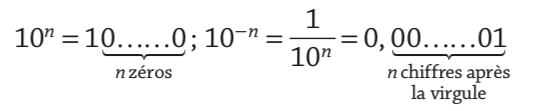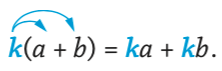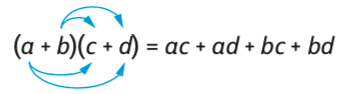Les puissances peuvent être utilisées pour faciliter l’écriture de nombres très petits ou très grands. En algèbre, on peut remplacer les nombres par des lettres. L’écriture des expressions littérales se transforme à l’aide de règles.
1 - Apprendre le cours
A - Les puissances
Définition
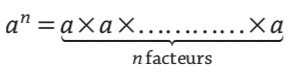
Le produit d’un nombre plusieurs fois par lui-même peut s’écrire sous forme d’une puissance de la façon suivante :
n étant un nombre entier supérieur à 1,
an se lit : « a puissance n ». On dit que a est élevé à la puissance n. Le nombre n est appelé exposant.
Par convention : a0 = 1 ; a1 = a ; a− n = 1/an (a ≠ 0).
Cas particuliers : a2 se lit « a au carré » ; a3 se lit « a au cube ».
Exemples
34 = 3 × 3 × 3 × 3 = 81 ; l’exposant de 34 est 4.
(− 4)3 = (− 4) × (− 4) × (− 4) = − 64 ; − 64 est le cube de − 4.
Les puissances de 10
Exemples
104 = 10 000 ; 106 = 1 000 000 = 1 million ; 109 = 1 000 000 000 = 1 milliard.
10− 3 = 0,001 = 1 millième
5 × 103 = 5 × 1 000 = 5 000 ; 7 × 10− 2 = 7 × 0,01 = 0,07
Dans un calcul, les puissances ont priorité sur les multiplications et les divisions.
B - La réduction d’expressions littérales
Réduire, c’est transformer une écriture pour la rendre plus simple.
On additionne les termes qui contiennent les mêmes lettres avec les mêmes exposants.
En l’absence de multiplication, on supprime les parenthèses.
Lorsqu’elles sont précédées d’un signe +, on les supprime sans changer les signes des termes placés dans les parenthèses.
Lorsqu’elles sont précédées d’un signe −, on les supprime en changeant les signes des termes placés dans les parenthèses.
Exemples
4x + 9x − x = 12x.
5y−8y2 +3+2y−4+y2 =−7y2 +7y−1.
(3u − 5) + (7 − 8u) + (− 4 + u) = 3u − 5 + 7 − 8u − 4 + u = − 4u − 2.
(3a − 5) − (7 − 8a) − (− 4 + a) = 3a − 5 − 7 + 8a + 4 − a = 10a − 8.
C - Le développement d'un produit
Développer un produit, c’est le transformer en une somme de termes.
Le produit d'un nombre par une somme
Quels que soient les nombres relatifs a, b, k, on a :
On dit que la
multiplication est distributive sur l’addition et la soustraction.
Exemple
Développer A = − 4(2x + 5) et B = x(2 − 3x).
A = (− 4) × 2x + (− 4) × 5 = − 8x – 20.
B = x × 2 + x × (− 3x) = 2x − 3x2.
Le produit d'une somme par une somme
Exemple
Développer et réduire E = (5x + 2)(3x + 4).
E = 5x × 3x + 5x × 4 + 2 × 3x + 2 × 4 = 15x2 + 20x + 6x + 8 = 15x2 + 26x + 8.
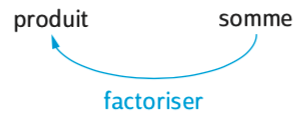
D - La factorisation
Factoriser une somme, c’est la transformer en produit.
Une des méthodes possibles pour factoriser une somme est la mise en facteur commun.
Exemples
15 + 3x = 3(5 + x) : on a mis 3 en facteur commun.
7x2 − 14x = 7x(x − 2) : on a mis 7x en facteur commun.
(3x − 1)(x + 6) + 5(3x − 1) = (3x − 1)(x + 6 + 5) = (3x − 1)(x + 11) : on a mis (3x − 1) en facteur commun.
Méthode : Comment mettre en facteur commun ?
Énoncé
Factoriser A = (x + 3)(2x + 5) − (x + 3)(x − 7).
Réponse
On écrit (x + 3) comme facteur commun : A = (x + 3)[(2x + 5) − (x − 7)]
On met dans le crochet « tout ce qui reste » une fois que (x + 3) est écrit.
On réduit l’expression entre les crochets après avoir supprimé les parenthèses :
A = (x + 3)(2x + 5 − x + 7)
A = (x + 3)(x + 12)
2 - Appliquer le cours
EXERCICES
Puissances
1. Calculer. Donner le résultat sous la forme d’une fraction lorsque c’est nécessaire.
a. 56 ; 65 ; 0,53 ; 172 ; 1,24.
b. (− 6)4 ; − 64 ; (− 4)5 ; − 45 ; 2− 3 ; 5− 2.
2. Écrire chaque nombre sous la forme d’une puissance de 10.
a. mille = 10... ; dix mille = ... ; un million = ... ; un milliard = ...
b. un centième = ... ; un millième = ... ; un millionième = ...
3. Calculer 7,2 × 105 ; 0,04 × 106 ; 13 × 10− 5 ; 0,8 × 10− 1.
Réduction d’expressions littérales
4. Réduire les expressions suivantes.
a.2x2 +5−3x2 +8 ;−3b+8−b−1+10b.
b. 2x2 − 7 + 3x − 8x + 5 + 4x2 ; 3v − v2 + 10 + v + 4 − 3v2.
5. Supprimer les parenthèses, puis réduire.
a.(5y−8)−(8y+3)+(−5y−3). b.2y−6+(−3y+5)−(−y−10).
c.2−8x+(1+2x2 −5x)−(x+x2 −3).
Développement
6. Dire si les expressions suivantes sont des sommes ou des produits.
A = 4x + 6 ; B = 5(a + 3) ; C = (2x + 1)(3x + 2) ; D = 8y2 + 5y + 3 ; E = a(2b + a).
7. Développer et réduire.
a. A = 2 − 3(8 − 9x) + 4(5 − 2x) ; B = 0,4(5x + 3) − 0,2(2x − 5) ;
C = 2x(3x − 5) − 4x(2x − 7).
b. D = (x + 2)(x − 3) ; E = (4x − 5)(x − 8); F = (2x − 3)(x + 0,5) ; G = (3x − 1)(3x − 1).
c. H = (− x + 4)(6x − 1) − 3(x2 + x − 2).
Factorisation
8. Factoriser les expressions suivantes.
A = 5x – 15y + 20 ; B = a5 + 7a3 ; C = 7x2 − 14x ; D = 28x3 + 14x2 − 7x.
9. Factoriser les expressions suivantes.
A = x(2x – 3) + 5(2x – 3) ; B = 2(2x + 1) + 3(2x + 1).
C = x(x + 3) – 8(x + 3) ; D = (3x – 2)(x + 4) – 5(x + 4).
E = (x − 1)(x + 1) + (x − 1)(2x + 5).
F = (2x + 3)(2x − 4) − (2x + 3)(x + 9).
CORRIGÉ
Puissances
1. a. 56 = 15 625 ; 65 = 7 776 ; 0,53 = 0,125 ; 172 = 289 ; 1,24 = 2,0736. 1 1
b. (− 6)4 = 1 296 ; − 64 = − 1 296 ; (− 4)5 = − 1 024 ; − 45 = − 1 024 ; 2− 3 = 1/8 ; 5− 2 = 1/25 .
2. a. mille = 103 ; dix mille = 104 ; un million = 106 ; un milliard = 109.
b. un centième = 10− 2 ; un millième = 10− 3 ; un millionième = 10− 6.
3. 7,2 × 105 = 720 000 ; 0,04 × 106 = 40 000 ; 13 × 10− 5 = 0,00013 ; 0,8 × 10− 1 = 0,08.
Réduction d’expressions littérales
4. a. 2x2 + 5 − 3x2 + 8 = − x2 + 13 ; − 3b + 8 − b − 1 + 10b = 6b + 7.
b. 2x2 − 7 + 3x − 8x + 5 + 4x2 = 6x2 − 5x – 2 ;
3v−v2 +10+v+4−3v2 =−4v2 +4v+14.
5. a. (5y − 8) − (8y + 3) + (− 5y − 3) = 5y − 8 − 8y − 3 − 5y − 3 = − 8y – 14.
b. 2y − 6 + (− 3y + 5) − (− y − 10) = 2y − 6 − 3y + 5 + y + 10 = 9.
c.2−8x+(1+2x2 −5x)−(x+x2 −3)=2−8x+1+2x2 −5x−x−x2 +3=x2 −14x+6.
Développement
6. A : somme ; B : produit ; C : produit ; D : somme ; E : produit.
7. a. A = 2 − 3(8 − 9x) + 4(5 − 2x) = 2 − 24 + 27x + 20 − 8x = 19x – 2.
B = 0,4(5x + 3) − 0,2(2x − 5) = 2x + 1,2 − 0,4x + 1 = 1,6x + 2,2.
C = 2x(3x − 5) − 4x(2x − 7) = 6x2 − 10x − 8x2 + 28x = − 2x2 + 18x.
b. D = (x + 2)(x − 3) = x2 − x − 6 ; E = (4x − 5)(x − 8) = 4x2 − 37x + 40.
F = (2x − 3)(x + 0,5) = 2x2 − 2x − 1,5 ; G = (3x − 1)(3x − 1) = 9x2 − 6x + 1.
c.H=(−x+4)(6x−1)−3(x2 +x−2)=−6x2 +25x−4−3x2 −3x+6=−9x2 +22x+2.
Factorisation
8. A = 5x – 15y + 20 = 5(x − 3y + 4) ; B = a5 + 7a3 = a3(a2 + 7) ;
C = 7x2 − 14x = 7x(x − 2) ; D = 28x3 + 14x2 − 7x = 7x(4x2 + 2x − 1).
9. A = x(2x – 3) + 5(2x – 3) = (2x − 3)(x + 5).
B = 2(2x + 1) + 3(2x + 1) = 5(2x + 1).
C = x(x + 3) – 8(x + 3) = (x + 3)(x − 8).
D = (3x – 2)(x + 4) – 5(x + 4) = (x + 4)(3x − 2 − 5) = (x + 4)(3x − 7).
E = (x − 1)(x + 1) + (x − 1)(2x + 5) = (x − 1)[(x + 1) + (2x + 5)] = (x − 1)(3x + 6).
F = (2x + 3)(2x − 4) − (2x + 3)(x + 9) = (2x + 3)[(2x − 4) − (x + 9)] = (2x + 3)(x − 13).