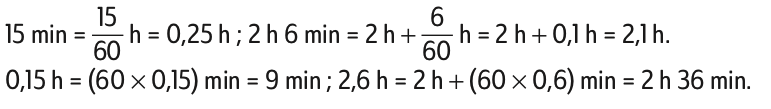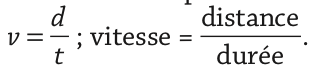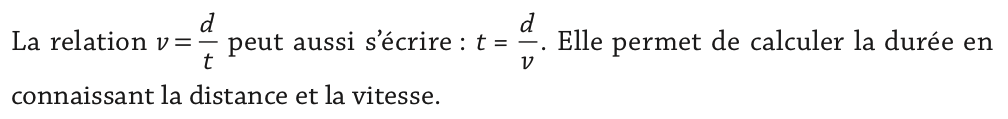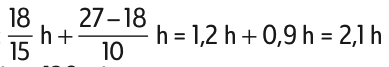Les unités de durée mesurent le temps que dure un événement : « Il m’a fallu 10 minutes pour répondre à cette question. » Le langage courant donne souvent le même sens aux mots temps et durée.
1 - Les durées
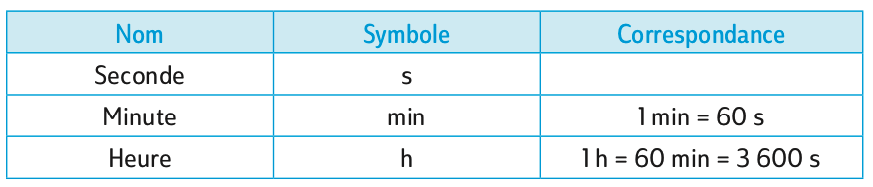
a) Le système sexagésimal
On utilise également le jour (j). 1 jour = 24 heures.
Exemples
2 h 51 min = (60 × 2) min + 51 min = 120 min + 51 min = 171 min.
4 h 32 min + 1 h 40 min = 5 h 72 min = 6 h 12 min.
4 h 32 min − 1 h 40 min = 3 h 92 min − 1 h 40 min = 2 h 52 min.
b) Le système décimal
Les durées peuvent également s’exprimer en utilisant des nombres décimaux. La partie entière d’une heure décimale est le nombre d’heures. Pour obtenir la partie décimale d’une heure décimale, on divise le nombre de minutes par 60. Inversement, pour obtenir le nombre de minutes, on multiplie la partie décimale par 60.
Exemples
2 - Les vitesses moyennes
a) Définition
La vitesse moyenne d’un mobile, c’est-à-dire d’un corps en mouvement, entre 2 points est la distance parcourue pendant une unité de temps. Les unités les plus courantes sont le kilomètre par heure (km/h) et le mètre par seconde (m/s).
b) La relation entre vitesse, distance et durée
Si d est la distance parcourue pendant une durée t par un mobile dont la vitesse moyenne est v, alors on a la relation :
Si d est en km et t en heures, alors v est en km/h.
Exemple
Sur terrain plat, un cycliste parcourt 52 km en 2 heures. Sa vitesse moyenne est : v = 52 / 2 = 26 km/h.
Pour une vitesse moyenne donnée, la distance parcourue est proportionnelle à la durée du parcours.
Exemple
À la vitesse moyenne de 16 km/h, la distance parcourue par un mobile en 1 h 30 min est : d = 16 × 1,5 = 24 km.
Attention à la cohérence des unités utilisées : si la vitesse est en km/h, la durée doit être en heure : 1 h 30 min = 1 h + 0,5 h = 1,5 h.
Exemple
Sur autoroute, un automobiliste a parcouru une distance de 270 km à la vitesse moyenne de 120 km/h. Quelle est la durée de son trajet en heures et minutes ?
t = d / v = 270 / 120 = 2,25h
t = 2h + 0,25 h = 2 h + (60 × 0,25) min = 2 h + 15 min = 2 h 15 min.
La durée du trajet est 2 h 15 min.
3) La conversion d'unité de vitesse
Pour passer d’une unité de vitesse à une autre :
- on convertit l’unité de longueur dans l’unité demandée ;
- on convertit l’unité de durée dans l’unité demandée ;
- on effectue le quotient des mesures obtenues.
Exemple
Convertir 27 km/h en m/min.
27 km = 27 000 m ; 1 h = 60 min.
27 km/h = 27 000 m / 60 min = 450 m/min.
Méthode : comment calculer une vitesse moyenne ?
Énoncé : Un véhicule roule pendant 3 heures ; il parcourt 182 km les 2 premières heures et 76 km la 3e heure. Calculer sa vitesse moyenne.
Réponse :
- On calcule la distance totale : 182 + 76 = 258 km.
- On calcule ou on relève la durée totale du parcours : 3 heures.
- On divise la distance par la durée : 258 / 3 = 86
La vitesse moyenne sur l’ensemble du parcours est 86 km/h.
EXERCICES
Durées
1. a. Convertir 2 h 31 min en minutes, puis en secondes. b. Convertir 53 min 38 s en secondes.
2. a. Convertir 528 min en heures et minutes.
b. Convertir 10 352 s en heures, minutes et secondes.
3. a. Donner l’écriture décimale de 3 h 48 min.
b. Donner l’écriture en heures et minutes de 5,70 h.
4. Calculer :
a. 4 h 25 min + 3 h 48 min ; 13 h 8 min 55 s + 2 h 25 s.
b. 56 min 12 s − 15 min 39 s ; 12 h − 4 h 16 min.
Vitesses moyennes
5. Un sprinter a couru 100 mètres en 10 s. Quelle est sa vitesse moyenne en km/h ?
6. Un train roule à la vitesse moyenne de 120 km/h. Quelle est la distance parcourue en 1 h 12 min ?
7. Un piéton marche à la vitesse moyenne de 5 km/h. Combien de temps mettra-t-il pour parcourir 14 km ?
8. Marc part de Lyon à 6 h 55 pour aller à Briançon. Son compteur marque 62 123 km. Il arrive à destination à 10 h 07. Son compteur affiche 62 339 km. Quelle est la vitesse moyenne de Marc ?
9. Un marcheur effectue une randonnée en utilisant une carte au 1/25 000e. Le trajet sur la carte mesure 84 cm. Il l’effectue à la vitesse moyenne de 3,5 km/h. Quelle est la durée de la randonnée ?
10. Parti à 9 h pour escalader à vélo le col de l’Izoard (27 km de long), j’ai parcouru les 18 premiers kilomètres à la vitesse moyenne de 15 km/h. La dernière partie étant plus dure, je l’ai effectuée à la vitesse moyenne de 10 km/h. Arrivé au sommet, j’ai pris 10 minutes de repos, puis je suis redescendu par la même route. Ma vitesse moyenne dans la descente a été le triple de celle de la montée. À quelle heure suis-je revenu ?
11. Un escargot avance à la vitesse constante de 3 m/h.
a. Quelle distance, en cm, a-t-il parcourue en 12 minutes ?
b. Combien de temps lui faut-il pour parcourir 2 m ?
12. Un automobiliste se déplace à la vitesse moyenne de 72 km/h. Il roule
de 7 h 45 min à midi. Quelle distance a-t-il parcourue ?
13. Le train n° 940 part de la gare de Mâcon à 7 h 35 min. Il arrive à la gare de Paris
à 9 h 20 min. Sachant que la distance entre Mâcon et Paris est 378 km, calculer la vitesse moyenne de ce train en km/h.
CORRIGÉ
Durées
1. a. 2 h 31 min = (60 × 2) min + 31 min = 120 min + 31 min = 151 min. 151 min = (60 × 151) s = 9 060 s.
b. 53 min 38 s = (60 × 53) s + 38 s = 3 180 s + 38 s = 3 218 s.
2. a. 528 ÷ 60 = 8 reste 48. Donc 528 min = 8 h 48 min.b. 10 352 ÷ 60 = 172 reste 32. 10 352 s = 172 min 32 s. Mais 172 min = 2 h 52 min. Donc 10 352 s = 2 h 52 min 32 s.
3. a. 48 min = (48/60)h = 0,8 h ; 3 h 48 min = 3 h + 0,8 h = 3,8 h.
b. 5,70 h = 5 h + (60 × 0,7) min = 5 h 42 min.
4. a. 8 h 13 min ; 15 h 9 min 20 s.
b. 40 min 33 s ; 7 h 44 min.
Vitesses moyennes
5. 100m / 10s = 10m/s = 36 000 m/h = 36 km/h.
6. Durée du parcours : 1 h 12 min = 1 h + (12/60)h = 1 h + 0,2 h = 1,2 h.
Distance parcourue : 120 × 1,2 = 144 km.
7. 14 ÷ 5 = 2,8 h = 2 h + (60 × 0,8) min = 2 h 48 min.
8. Distance parcourue : 216 km ; durée du parcours : 3 h 12 min = 3,2 h. Vitesse moyenne : 216 ÷ 3,2 = 67,5 km/h.
9. Longueur du trajet : 84 × 25 000 = 2 100 000 cm = 21 km.
Durée : 21 ÷ 3,5 = 6 h. 18
10. Durée de la montée :
= 120 min + (0,1 × 60) min = 126 min.
Durée de la descente : 126 ÷ 3 = 42 min.
Durée de la sortie : 126 min + 42 min + 10 min = 178 min = 2 h 58 min. Heure du retour : 9 h + 2 h 58 min = 11 h 58 min.
11. a d = 3 x (12/60) = 0,6 m = 60 cm
b. t = (2/3)h = 60 x 2/3 = 40 min
12. Durée du déplacement : 12 h − 7 h 45 min = 4 h 15 min = 4,25 h.
d = 72 × 4,25 = 306 km.
13. Durée du parcours : 9 h 20 min − 7 h 35 min = 1 h 45 min = 1,75 h.
Vitesse moyenne : 378 / 1,75 = 216 km/h.