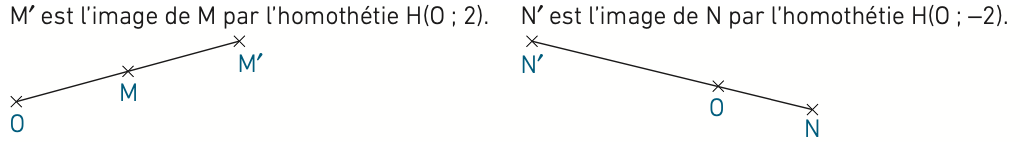L’homothétie est une autre transformation particulière du plan qui, contrairement aux symétries, translations et rotations, transforme vraiment la figure. En effet, l’image d’une figure par une homothétie (de rapport différent de 1) n’est pas superposable avec cette figure. L’homothétie n’est pas une isométrie.
I) La leçon
1) Définition
Étant donnés un point O et un nombre non nul, on appelle homothétie de centre O et de rapport , que l’on note H(O, ), la transformation qui, à tout point M (autre que O), associe un point M′ tel que :
– les points O, M et M′ sont alignés ;
– si , alors M′ est sur la demi-droite [OM) tel que ;
– si , alors M′ est sur la demi-droite [MO) sans être sur le segment [OM] tel que .
O est sa propre image.
Exemple :
2) Propriétés
L’homothétie conserve l’alignement, les milieux, les angles, l’orthogonalité, le parallélisme mais pas les longueurs (sauf si le rapport est égal à 1). En revanche, l’homothétie conserve l’égalité des longueurs, c’est-à-dire que des segments ont pour image des segments de même longueur.
L’image d’une droite par une homothétie est une droite qui lui est parallèle.
Conséquences : une homothétie de rapport ou agrandit une figure. Une homothétie de rapport tel que réduit une figure.
II) Ce qu'il faut savoir faire
Reconnaitre si deux figures sont images l’une de l’autre par une homothétie
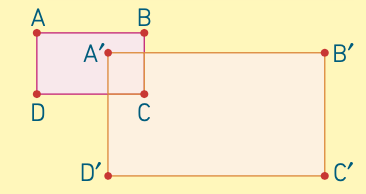
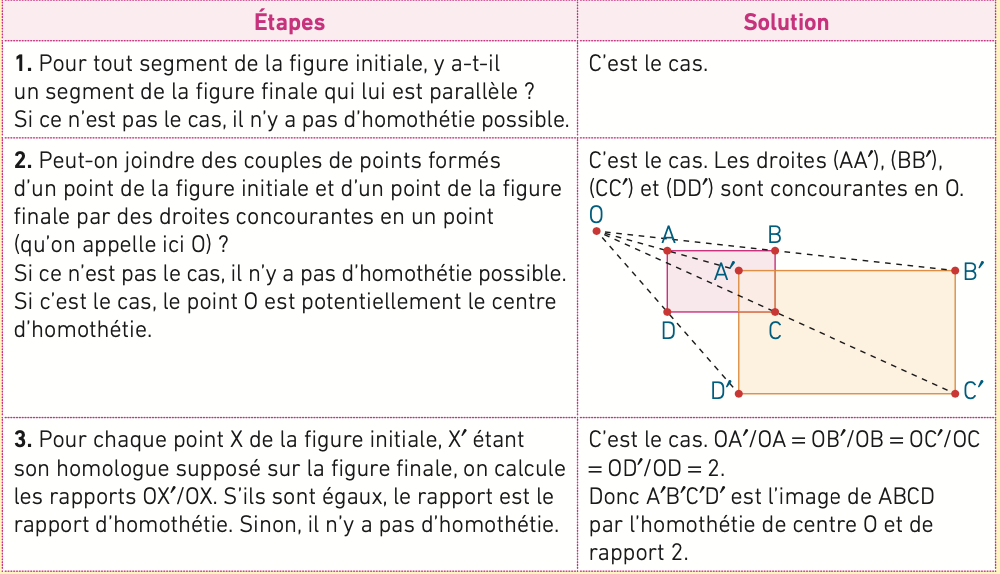
Exemple : A′B′C′D′ est-il l’image de ABCD par une homothétie ? Si oui, caractériser cette homothétie.
Construire l’image d’une figure par une homothétie donnée
On peut tracer les images des points caractéristiques de la figure (sommets des polygones, centre des cercles...) et on complète la figure en utilisant les propriétés de conservation citées ci-dessus.
III) Je m'entraine
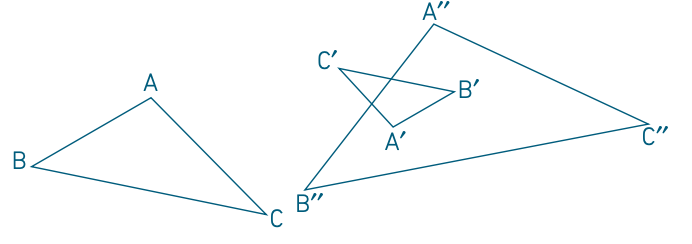
1. a. Le triangle A′B′C′ est-il l’image du triangle ABC par une homothétie ? Si oui, caractériser cette homothétie.
b. Le triangle A′′B′′C′′ est-il l’image du triangle ABC par une homothétie ? Si ce n’est pas le cas, est-il un agrandissement du triangle ABC ?
2. Tracer un triangle ABC tel que AB = 5 cm, BC = 4 cm et AC = 3,5 cm. Placer un point D à l’intérieur du triangle tel que AD = 2,5 cm et BD = 3 cm. Tracer en rouge l’image de ABC par H(D, 1,5).