Reconnaitre des grandeurs proportionnelles (ou une situation de proportionnalité) permet de traiter différents types de problèmes.
I) Leçon
1. Définitions
Deux grandeurs sont proportionnelles si on peut calculer les valeurs de l’une en multipliant par un même nombre a les valeurs de l’autre. Ce nombre a est appelé coefficient de proportionnalité.
Conséquences :
- la proportionnalité entre deux grandeurs peut être modélisée par une fonction linéaire, donc du type ;
- dans une situation de proportionnalité, les deux suites obtenues par la mise en relation de valeurs qui se correspondent sont des suites proportionnelles.
2. Propriétés
Deux propriétés importantes des grandeurs proportionnelles sont présentées ici. D’autres découlent de l’étude des suites proportionnelles.
a. Propriété additive de linéarité
Si deux grandeurs sont proportionnelles, à la somme de deux valeurs de la 1re grandeur correspond la somme des valeurs correspondantes de la 2de grandeur, ce qui est illustré dans le tableau.
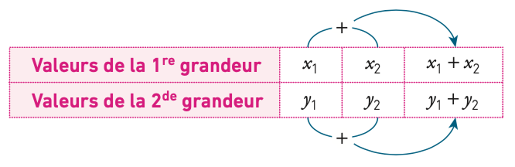
ATTENTION : La réciproque est fausse.
Exemple : On a construit des tours avec des cubes tous identiques. On a mesuré la hauteur des tours construites avec 7 cubes et avec 9 cubes. On peut en déduire la hauteur d’une tour qui serait construite avec 16 cubes. Il n’est pas nécessaire de connaitre la hauteur d’un cube.
b. Propriété multiplicative de linéarité
Si deux grandeurs sont proportionnelles, au produit par un nombre d’une valeur de la 1re grandeur correspond le produit par ce même nombre de la valeur correspondante de la 2de grandeur, ce qui est illustré dans ce tableau.

Exemple : Si on connait la hauteur d’une tour de 7 cubes, on peut en déduire celle d’une tour construite avec 14 cubes. À nouveau, il n’est pas nécessaire de connaitre la hauteur d’un cube.
II) Ce qu'il faut savoir faire
Calculer le coefficient de proportionnalité connaissant des valeurs qui se correspondent pour deux grandeurs proportionnelles
Il suffit de calculer le rapport entre une valeur de la 2de grandeur et la valeur qui lui correspond pour la 1re grandeur.
Exemple (suite) : on calcule par exemple . C’est aussi, en cm, la hauteur d’un cube.
Reconnaître si deux grandeurs sont proportionnelles
Soit on utilise une connaissance sociale ou expérimentale, soit on met en évidence l’existence du coefficient de proportionnalité entre les deux grandeurs.
Exemple : le périmètre p d’un carré est proportionnel à son côté c.
On sait que , ce qui fait apparaitre le coefficient de proportionnalité (4).
Reconnaître que deux grandeurs ne sont pas proportionnelles
On peut :
- soit mettre en évidence que les rapports de deux couples de valeurs qui se correspondent ne sont pas égaux ;
- soit mettre en évidence un contre-exemple qui montre que l’une ou l’autre des propriétés de linéarité n’est pas vérifiée.
III) Je m'entraîne
1. Le volume d’un cylindre se calcule à l’aide de la formule : (r étant le rayon de sa base et h sa hauteur). Le volume d’un cylindre est-il proportionnel au rayon de sa base ? À sa hauteur ?
2. Y a-t-il proportionnalité entre :
a. l’âge d’un enfant et sa taille ?
b. la masse d’un tas de pièces toutes identiques et le nombre de pièces ?


