Fonction affine

Dans un système d’axes perpendiculaires gradués régulièrement à partir de 0, les couples de nombres correspondants sont représentés par des points alignés.

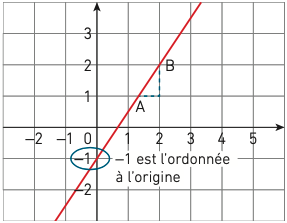
La courbe représentative d’une fonction affine est donc une droite d’équation $y=ax+b$ qui passe par le point de coordonnées (0 ; $b$). Le nombre $b$ est appelé ordonnée à l’origine.

Exemple : Représentation graphique de la fonction f telle que $\text{f}(x)=\frac{3}{2}x-1$

Le nombre $a$ est appelé coefficient directeur de la droite. Il caractérise la « pente » de la droite qui représente la fonction, c’est-à-dire son inclinaison par rapport à l’axe des abscisses.

Ce coefficient directeur $a$ est égal à la variation de l’ordonnée lorsque l’abscisse augmente de 1. En effet, $\text{f}(x+1)-\text{f}(x)=a(x+1)-ax=a$.

Exemple : Lorsqu’on passe du point A (1 ; $\frac{1}{2}$) au point B (2 ; 2), l’abscisse augmente de 1 et l’ordonnée de $\frac{3}{2}$ (ou 1,5) (cf. passage du point A au point B sur la représentation graphique).

Si a>0, la fonction affine est croissante.
Si a<0, la fonction affine est décroissante.

Dans l’exemple, la droite représente la fonction f telle que $\text{f}(x)=\frac{3}{2}x-1$ et a pour équation $y=\frac{3}{2}x-1$.

II) Ce qu'il faut savoir faire

Représenter graphiquement une fonction affine

Exemple : représenter graphiquement la fonction

$f:\text{R}\longrightarrow\text{R}$

$x\longmapsto -2x+\frac{1}{2}$

Déterminer l’expression algébrique d’une fonction affine connaissant la droite qui la représente

La fonction associée est de la forme $\text{f}(x)=ax+b$. Deux méthodes sont possibles :
– utiliser les coordonnées de deux points de la droite dont les coordonnées ($x_1$ ; $y_1$) et ($x_2$ ; $y_2$) sont faciles à lire et les égalités $y_1 =ax_1 +b$ et $y_2 =ax_2 +b$, ce qui donne
un système de deux équations d’inconnues $a$ et $b$ ;

– lire l’ordonnée à l’origine qui donne la valeur de b et déterminer a en augmentant de 1 l’abscisse d’un point et en cherchant la variation correspondante de son ordonnée.

III) Je m'entraine

1. Parmi ces fonctions, lesquelles sont des fonctions affines ?

$f:\text{R}\longrightarrow\text{R}$

$x\longmapsto 3-x$

$g:\text{R}\longrightarrow\text{R}$

$x\longmapsto \frac{x-4}{3}$

$h:\text{R}\longrightarrow\text{R}$

$x\longmapsto \frac{\sqrt{2}}{2}x$

$i:\text{R}\longrightarrow\text{R}$

$x\longmapsto x^2-x$

2. Pour celles qui sont des fonctions affines, tracer leur représentation graphique.

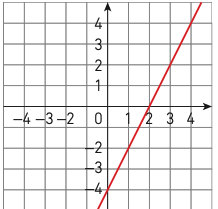
3. Donner l’expression algébrique de la fonction représentée par cette droite.