D’autres objets de géométrie et éléments de vocabulaire et de syntaxe associés sont présentés.
I) Leçon
1) Droites perpendiculaires, droites parallèles
A) Définitions, notations
Deux droites perpendiculaires sont deux droites sécantes qui forment un angle droit (angle de 90°) donc quatre angles droits.
Exemple :
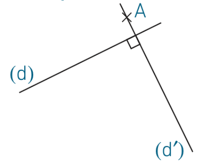
Les droites (d) et (d′) sont perpendiculaires.
La droite (d′) est la droite perpendiculaire à (d) qui passe par le point A. On note : (d) ⊥ (d′).
Deux droites parallèles sont deux droites confondues ou deux droites qui n’ont aucun point commun.
Exemple :
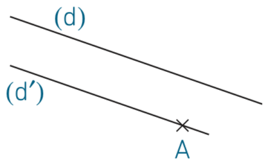
Les droites (d) et (d′) sont parallèles.
La droite (d′) est la droite parallèle à (d) qui passe par le point A. On note : (d) // (d′).
B) Propriété
Si deux droites sont perpendiculaires à une même troisième, alors elles sont parallèles. Cette propriété permet de tracer des droites parallèles, de vérifier et de démontrer que deux droites sont parallèles.
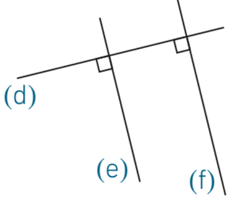
Exemple : (e) et (f) sont deux droites parallèles car elles sont toutes les deux perpendiculaires à (d).
2) Médiatrice d’un segment
La médiatrice d’un segment est l’ensemble des points équidistants des extrémités de ce segment.
« Équidistant » signifie « à même distance ».
C’est la droite qui passe par le milieu du segment et qui est perpendiculaire à ce segment.
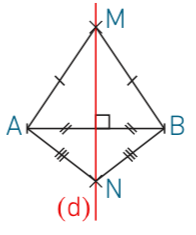
Exemple : (d) est la médiatrice du segment [AB].
II) Ce qu'il faut savoir faire
➢ Décrire une figure en utilisant le vocabulaire et les notations de géométrie
➢ Tracer la médiatrice d’un segment
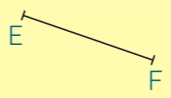
Exemple : tracer la médiatrice du segment [EF].
Méthode 1 : avec l’équerre et la règle graduée, on place le milieu du segment et on trace la perpendiculaire.
Méthode 2 : avec le compas.
Justification : les points d’intersection sont, par construction, équidistants des extrémités du segment. Ils sont donc sur la médiatrice du segment. Or, comme il y a une seule droite passant par deux points, c’est la médiatrice du segment.
III) Je m'entraîne
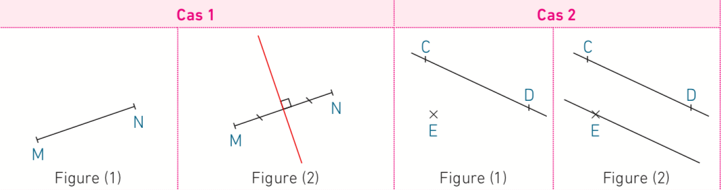
1. Dans chaque cas, trouver l’instruction à communiquer pour passer de la figure (1) à la figure (2).
2. Construire un triangle ABC. Tracer, en utilisant la règle graduée et l’équerre, la médiatrice de [AB] et, en utilisant le compas, les médiatrices de [BC] et de [AC].