Diagrammes et histogrammes

I) Les points clés

1) Diagrammes

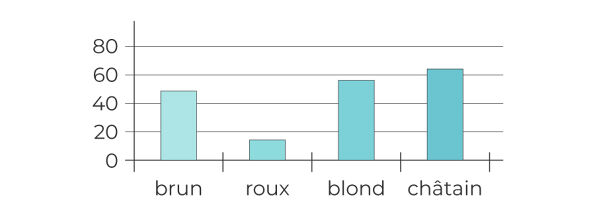
Un diagramme en bâtons (ou barres) est composé de bâtons. Leur hauteur est proportionnelle à l'effectif (ou à la fréquence) représenté(e).

Exemple : on répartit des élèves de 5^e en fonction de leur couleur de cheveux.

Un diagramme circulaire est un disque partagé en secteurs angulaires. La mesure de l'angle de chaque secteur est proportionnelle à l'effectif (ou à la fréquence) représenté(e).

Mots-clés

• Amplitude : L'amplitude d'une classe est la différence entre la plus grande et la plus petite valeur de la classe.
• Secteur angulaire : Il s'agit d'une « part » d'un disque.

2) Histogrammes

On utilise un histogramme pour représenter une série regroupée en classes.

Un histogramme est composé de rectangles qui ont une largeur égale à l'amplitude de la classe. La hauteur de chaque rectangle est proportionnelle à l'effectif de la classe représentée.

Exemple : voici la répartition d'élèves de 5^e en fonction de leur taille (l'amplitude de chaque classe est égale à 5 cm).

II) Construire un diagramme circulaire

On a interrogé 150 personnes sur leur lieu de vacances.

1. Je calcule le coefficient de proportionnalité. L'effectif total (150 personnes) correspond à un angle de 360°, donc le coefficient de proportionnalité est : $\dfrac{360}{150} = 2,4$

2. Je calcule les mesures des angles : $51 \times 2,4 = 122,4°$, etc.

3. Je construis le diagramme à l'aide d'un rapporteur.