Cylindre, cône, sphère et éléments de géométrie dans l’espace

Cette fiche présente trois nouveaux solides usuels qui ne sont pas des polyèdres et aborde également les notions de droites et plans parallèles et perpendiculaires.

I) Leçon

1. Plans et plans parallèles

$\rightarrow$ Un plan dans l’espace est représenté généralement par un parallélogramme.

Information pratique
On peut imaginer un plan comme étant une plaque très fine rigide dont on peut augmenter autant que l’on veut les dimensions.

$\rightarrow$ Deux plans non confondus sont parallèles s’ils n’ont aucun point commun.
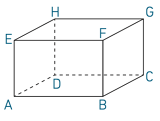
Exemple : Dans le pavé ci-contre, les plans ABCD et EFGH sont parallèles.

2. Autres solides usuels

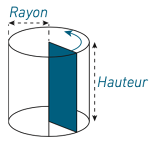
$\rightarrow$ Un cylindre de révolution (appelé plus simplement cylindre) est un solide obtenu en faisant tourner un rectangle autour de l’un de ses côtés. Il possède deux bases identiques et parallèles, qui sont des disques. La distance entre les deux bases est appelée hauteur. La droite joignant les centres des disques de base est perpendiculaire aux bases.

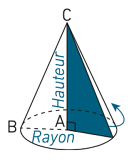
$\rightarrow$ Un cône de révolution (appelé plus simplement cône) est un solide obtenu en faisant tourner un triangle rectangle autour de l’un des côtés de l’angle droit. La base est donc un disque. La droite qui joint le sommet du cône au centre du disque est perpendiculaire au plan de base.

$\rightarrow$ O étant un point et r un nombre réel positif, la sphère de centre O et de rayon r est l’ensemble des points de l’espace tels que la distance de ces points à O est égale à r.
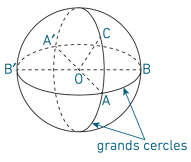
On appelle grand cercle de cette sphère tout cercle de centre O et de rayon r. Les points d’un grand cercle appartiennent à la sphère.
Exemple : Sur la figure ci-dessous, on a OA = OA′ = OB = OB′ = OC = rayon de la sphère.

3. Droites perpendiculaires, orthogonales dans l’espace

$\rightarrow$ Deux droites de l’espace sont perpendiculaires si elles sont dans le même plan (on dit qu’elles sont coplanaires) et forment un angle droit (donc quatre).
Exemple : Dans le pavé du paragraphe 1, les droites (FG) et (FB) sont perpendiculaires.

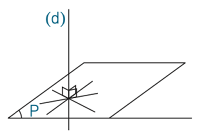
$\rightarrow$ P1 : une droite orthogonale à un plan est une droite qui coupe le plan en un point et qui est perpendiculaire à toutes les droites du plan qui passent par ce point.

$\rightarrow$ P2 : si une droite coupe un plan en un point et si elle est perpendiculaire à deux droites de ce plan, alors elle est orthogonale à ce plan (donc elle est perpendiculaire à toutes les droites de ce plan qui passent par ce point d’intersection).

II) Ce qu'il faut savoir faire

$\Rightarrow$ Démontrer qu’une droite est perpendiculaire à une autre dans l’espace en utilisant les propriétés des solides
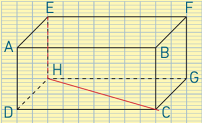
Exemple : ABCDEFGH est un pavé droit. Démontrer que (EH) et (HC) sont perpendiculaires.

III) Je m'entraîne

1. SABCD est une pyramide régulière de sommet S et de base carrée ABCD. Soit O l’intersection des diagonales du carré. Démontrer que (SO) et (OA) sont perpendiculaires.

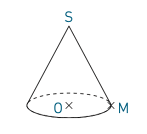
2. Le cône ci-dessous a pour sommet S et pour rayon 2 cm. On sait que SM = 4 cm. Calculer la hauteur de ce cône.