Aire de figures usuelles

Il n’existe pas d’instrument pour mesurer les aires. Un calcul est donc toujours nécessaire.

I) Leçon

1. Mesure de l’aire d’une surface

$\rightarrow$ Une unité étant choisie, la mesure de la longueur d’une ligne est le nombre d’unités nécessaires qu’il faut reporter pour la recouvrir entièrement.

$\rightarrow$ Conséquence : la mesure est un nombre réel qui dépend du choix de l’unité de mesure.
Exemple : En cm², la mesure de l’aire de la surface S est 6,25. En mm², la mesure de l’aire de la surface S est 625. On dit aussi que l’aire de la surface S est égale à 6,25 cm² ou à 625 mm². On a donc l’égalité 6,25 cm² = 625 mm².

Pour calculer rapidement et facilement l'aire d'une surface, n'hésite pas à utiliser notre outil !

2. Aire des figures usuelles

Dans la suite, l’aire de la figure est désignée par A.

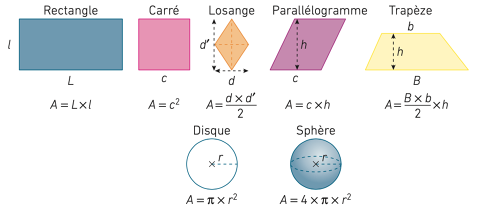
a. Aire de quelques quadrilatères, du cercle, du disque et de la sphère

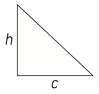
b. Aire du triangle

$\rightarrow$ $A=\frac{\text{côté}\times\text{hauteur associée à ce côté}}{2}$.
Un triangle possède trois hauteurs. Il y a donc trois possibilités :

$\rightarrow$ Cas particulier du triangle rectangle : l'un des côtés de l'angle droit est une hauteur par rapport à l’autre côté de l’angle droit.

3. Unités d’aire

$\rightarrow$ Les unités d’aire sont définies par le Système international d’unités (SI). L’unité principale est le mètre-carré égal à l’aire d’un carré de 1 m de côté. Les différentes unités sont liées entre elles par des relations liées au système décimal.

$\rightarrow$ Les mesures de terrains sont souvent exprimées dans un système dont l’unité principale est l’are (a). Les autres unités utilisées sont l’hectare $(1\rm\ ha = 100\rm\ a)$ et le centiare $(1\rm\ ca = \frac{1}{100}a)$.

$\rightarrow$ Les deux systèmes d’unité sont liés par l’égalité 1 a = 1 dam² = 100 m².

$\rightarrow$ Ces deux systèmes sont présentés dans le tableau suivant :

On remarque que 1 ha = 1 hm² et 1 ca = 1m².

Attention : Dans le 1^er système (en m²), une unité située à gauche d’une autre unité dans le tableau vaut 100 fois cette unité. Exemple : 1 km² = 100 hm² = 10 000 dam²...

II) Ce qu'il faut savoir faire

$\Rightarrow$ Calculer l’aire d’une figure usuelle ou une longueur dans une figure usuelle dont l’aire est connue
On utilise les formules connues.

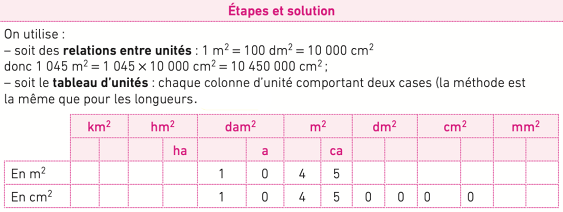
$\Rightarrow$ Effectuer des conversions d’unités
Exemple : convertir 1 045 m² en cm² .

III) Je m'entraîne

Calculer l’aire en cm² de ce triangle et de ce parallélogramme.