La notion d’échelle est utilisée pour représenter un objet ou espace réel en réduction ou en agrandissement, en respectant les proportions entre ses dimensions.
I) La leçon
1) Définition
On appelle échelle de la représentation d’un objet le rapport k entre les dimensions sur la représentation (maquette, carte, plan...) et les dimensions réelles (les dimensions étant exprimées dans la même unité).
On a donc la formule k=dD, d et D représentant respectivement les dimensions sur la
représentation et les dimensions dans la réalité, exprimées avec la même unité de mesure.
Si \mathbf{k>1}, on a un agrandissement ; si \mathbf{k<1}, on a une réduction.
Dans le cas d’une réduction, l’échelle est généralement exprimée par une fraction de numérateur 1, donc de la forme 1e.
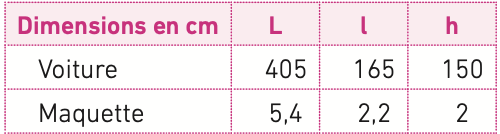
Exemple : La maquette d’une voiture de dimensions 4,05 m (longueur), 1,65 m (largeur) et 1,5 m (hauteur) a pour dimensions 5,4 cm (longueur), 2,2 cm (largeur) et 2 cm (hauteur). Le tableau suivant rend compte de la situation.
Les rapports 5,4405, 2,2165 et 2150 sont égaux à 175.
L’échelle de la maquette (qui est une réduction) est donc 175 (lue un soixante-quinzième).
Autrement dit, 1 cm sur la maquette représente 75 cm dans la réalité.
Il y a proportionnalité entre les longueurs sur la représentation et les longueurs « dans la réalité », k étant le coefficient de proportionnalité (dans l’exemple, k=175).
Dans un agrandissement ou une réduction, les angles sont conservés.
II) Ce qu'il faut savoir faire
On envisage 3 types de problèmes :
– calculer une distance dans la réalité, l’échelle et la distance sur la représentation étant connues ;
– calculer une distance sur la représentation, l’échelle et la distance dans la réalité étant connues ;
– calculer une échelle la distance dans la réalité et la distance sur la représentation étant connues.
Pour les résoudre, on utilise la même méthode : on écrit la formule : k=dD
• Étape 1 : on remplace les grandeurs dont on connait la valeur par cette valeur, après avoir exprimé, si nécessaire, les longueurs dans la même unité.
• Étape 2 : on effectue les calculs ou on résout l’équation obtenue pour obtenir la valeur cherchée.
Calculer une distance dans la réalité
Exemple : sur un plan à l’échelle 12500, une rue mesure 24 cm de long. Quelle est la longueur réelle de cette rue ?
Calculer une distance sur une représentation
Exemple : une fusée de 12 m de haut est représentée par une maquette réalisée à l’échelle 1150. Quelle est la hauteur de la maquette ?
Calculer une échelle
Exemple : la distance à vol d’oiseau entre deux villes est de 105 km. Sur une carte, elle correspond à une distance de 14 cm. Quel est l’échelle de cette carte ?
III) Je m'entraine
1. Un microscope fournit une image de 4 cm pour un objet de 1 mm. Quelle est l’échelle utilisée ?
2. Sur une carte réalisée à l’échelle 1125000 :
a. Quelle distance réelle correspond à 16 cm sur la carte ?
b. Quelle distance sur la carte correspond à 35 km dans la réalité ?