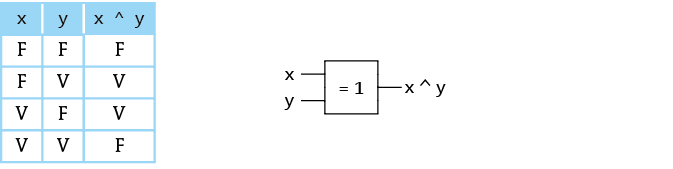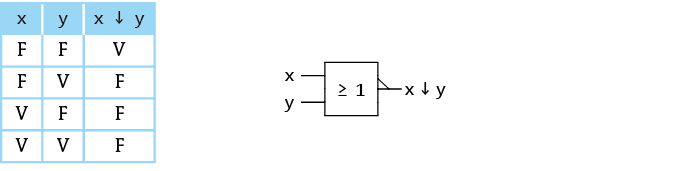Les propriétés et les lois de l’algèbre de Boole sont utiles pour travailler sur des fonctions plus complexes combinant les opérations fondamentales de l’algèbre booléenne.
I. Les lois de l’algèbre de Boole
Les lois suivantes sont facilement démontrables à l’aide de tables de vérités.
|
Propriété |
Signification |
|
Commutativité |
x | y = y | x et x & y = y & x |
|
Associativité |
x | (y | z) = (x | y) | z et x & (y & z) = x & (y & z) |
|
Distributivité |
x & (y | z) = (x & y) | (x & z) et x | (y & z) = (x | y) & (x | z) |
|
Élément neutre |
x | F = x et x & V = x |
|
Élément absorbant |
x & F = F |
|
Involution |
~(~x) = x |
|
Tiers-exclus |
~x | x = V |
|
Non-contradiction |
~x & x = F |
|
Idempotence |
x & x = x et x | x = x |
|
Lois de De Morgan |
~(x | y) = ~x & ~y et ~(x & y) = ~x | ~y |
II. Les fonctions composées
Toutes les opérations booléennes peuvent s’écrire en n’utilisant que les trois opérateurs &, | et ~. Mais en pratique on utilise aussi d’autres fonctions logiques, qui s’obtiennent à partir des opérations fondamentales.
1) Disjonction exclusive (ou exclusif, xor)
x ^ y = (x & ~y) | (~x & y)
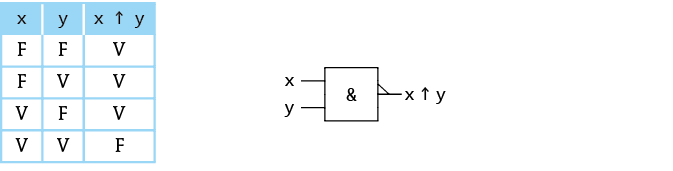
2) Non Et (nand)
x ↑ y = ~(x & y)
3) Non Ou (nor)
x ↓ y = ~(x | y)
À noter
On peut montrer que toutes les fonctions logiques précédentes peuvent s’obtenir à partir de la seule fonction Nand.
III. Opérations bit à bit
On peut généraliser les opérations précédentes à des chaînes de bits.
Exemples :
|
Addition posée |
Avec Python |
|
1011011 & 1010101 -------------------- 1010001 |
>>> bin(0b1011011 & 0b1010101) '0b1010001' |
|
1011011 | 1010101 -------------------- 1011111 |
>>> bin(0b1011011 | 0b1010101) '0b1011111' |
|
1011011 ^ 1010101 -------------------- 0001110 |
>>> bin(0b1011011 ^ 0b1010101) '0b1110' |